“La Musica è un esercizio aritmetico della mente che conta senza sapere di contare” (Musica est exercitium arithmeticae occultum nescientis se numerare animi) scriveva Leibniz, rifacendosi alle teorie pitagoriche secondo cui il segreto dell’armonia risiede nel potere magico dei numeri.
Ascoltare una bella melodia e pensare che risponda a specifici rapporti matematici è qualcosa di molto astratto, soprattutto per chi non è un musicista. Studiando la teoria musicale si scopre come tutto segua delle regole precise. Nel Medioevo, ad esempio, la Musica (“ars musica”) veniva insegnata nel Quadrivio insieme alle discipline attribuite alla sfera matematica (aritmetica, geometria, astronomia).
La Musica può essere descritta in senso formale come una serie di eventi sonori disposti nel tempo: ogni nota ha una sua funzione perché inserita all’interno di un sistema di relazioni spiegato dalla scienza dell’armonia. Ad esempio, nel sistema musicale occidentale possiamo pensare alla scala di Do maggiore, costituita da 7 suoni diversi per numero di vibrazioni (la frequenza) ai quali per convenzione diamo i nomi di: Do, Re, Mi, Fa, Sol, La Si.
Come gradini di una scala, questi 7 suoni sono distanti tra loro e la distanza tra un suono e l’altro viene chiamata “intervallo” che quindi rappresenta la differenza di altezza tra due note.
Tornando alla nostra scala di Do maggiore: Do, Re, Mi, Fa, Sol, La Si e poi nuovamente Do (se vogliamo proseguire e salire sempre di più) il secondo Do è un suono diverso dal primo, è più acuto. Porta sempre il nome di Do perché ha una somiglianza speciale con il primo: ha un numero doppio di vibrazioni per secondo (stanno in rapporto di 2:1) e si dice per convenzione che è all’ottava superiore del primo (in quanto è l’ottavo suono dopo il Do iniziale). Tra Do e Re c’è un intervallo di seconda, tra Do e Mi di terza, tra Do e Fa di quarta e via dicendo.

La distanza tra due note quindi è definita da un ben determinato rapporto numerico: il rapporto delle frequenze di quelle due note. Il discorso è molto complicato da spiegare brevemente, ma spero questo accenno possa far intuire come i suoni delle scale musicali siano collegati tra loro da precisi rapporti matematici.
I rapporti tra le note creano armonia non solo all’udito, ma anche nella forma ed esiste un modo per vedere queste misteriose frequenze e il rapporto magico che creano tra di loro.
Guardate com’è il rapporto di ottava, la distanza tra i due Do di cui parlavamo prima.
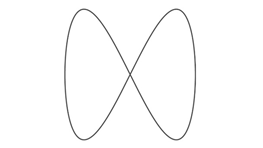
Ricorda il numero otto e anche il simbolo dell’infinito. Questa scoperta si deve al matematico francese Jules Lissajous, che a metà del XIX secolo scoprì come proiettare una vibrazione sonora su uno schermo. L’esperimento consiste nel proiettare un raggio luminoso tra le forcelle di un diapason (uno strumento musicale di metallo a forma di U che vibrando produce suoni di un’altezza perfettamente determinata); con un gioco di specchi, il raggio riflette la vibrazione su uno schermo producendo un’onda sinusoidale.
Aggiungendo un altro diapason e sommando due diverse vibrazioni Lissajous scoprì che producevano forme bellissime, oggi conosciute come “figure di Lissajous”, possono essere considerate come l’espressione geometrica dell’armonia musicale.
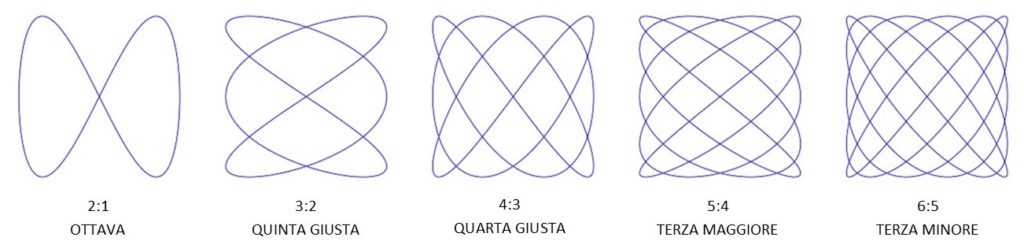
Erano le prime immagini dell’armonia. Dopo tanta teoria Lissajous ha dimostrato come l’unione di due particolari note in “armonia” tra loro crea non solo suoni armonici, ma anche forme armoniche.
La musica deriva da principi matematici capaci di creare complessità, armonia, varietà e bellezza.
A questo link viene riproposto l’esperimento di Lissajous con i due diapason e il gioco di specchi, proprio come doveva averlo ideato lo scienziato francese.
Mentre grazie alla tecnologia oggi possiamo osservare queste particolari onde con immagini più chiare e dirette:
Infine, una vera magia.





No Comments